Motion Estimation

Contents

All methods described here are for natural images and are unlikely to work well with synthetic images. Code has all been tested on Linux; some knowledge of docker, git, Python and C++ is assumed.

Global Motion Estimation

Introduction

Phase correlation is one technique that can be used to find the global alignment between two images quickly. This is an example of direct motion estimation because it operates directly on the pixel values.

Images are transformed to the frequency domain, therefore a window must be applied to the images to avoid the edges from correlating and resulting in zero motion. Unfortunately, the windowing reduces the maximum amount of motion that can be measured.

The output of phase correlation is a surface where conveniently the height represents the confidence and the location represents the motion.

Phase correlation is usually used to find translation but can be extended to find rotation and scale. For other motion models it is possible to use pixel difference gradients to optimise the motion model. If there is a lot of local motion or depth in the scene then indirect motion estimation using features can be better.

Pros

Cons

Implementation

  1. Load the images and convert to luminance (or grey)
  2. Apply windowing
  3. Compute the phase correlation surface and find the location of the peak

  Code on github

Example

These are 2 images that we will will use to test our approach with, the camera was panning to the right in this shot and the images are 5 frames apart:

Frame 155
Frame 160

Calculate the phase correlation between these 2 images:

pc.py --current frame_00160.png --previous frame_00155.png

This produces the following output:

Detected shift: (14.143573237407736, -0.13359329274885567), Correlation: 0.8721376508547936

Composite the 2 images into the same co-ordinate frame:

globalmc.py --current frame_00160.png --previous frame_0155.png --xoff 14.143573237407736 --yoff -0.13359329274885567 --output aligned.png

Here is the composited output:

Aligned images

It's a pretty good result for non-consecutive images. All the detail from the image on the right are visible on the right edge and on the left edge there is detail added from the left image.

Some discontinuities can be seen at the edges of combined images due to rotation of the camera, lens distortion. objects at different depths in the scene (parallax) and local object motion. Other methods may use motion or camera models that can account for these effects.

Summary

Local Motion Estimation

Introduction

Local motion estimation is a core algorithm for video compression via motion compensation and residual encoding. Block matching algorithms divide frames into a grid of blocks and search for matches in another frame. This method is used in video coding standards such as MPEG-4/H.264, HEVC/H.265 and VVC/H.266.

Pros

Cons

Implementation

  Code on github

There are many choices for the block search algorithm, usually resulting in a trade off between image quality and speed. Selection is determined by whether the algorithm will be implemented in software, ASIC or FPGA and whether it is needed for offline or online use.

There are 2 algorithms implemented here: the two dimensional full search (2DFS), a brute force approach and PMVFAST, an algorithm that uses predictors based on spatio-temporally neighbouring blocks, the median vector and early search termination combined with small or large diamond search patterns.

In the PMVFAST paper we can infer that the authors use a block size of 16×16 pixels and the threshold values they give are based on this size. In modern video coding standards blocks can be other sizes and can also be subdivided.

Example

Using the full search, find the motion vectors between two images; apply motion compensation to produce a prediction of the current image using only the previous image:

bma -c current.jpg -p previous.jpg -v motion.mv
bmc -p previous.jpg -v motion.mv -o compensated_current.jpg

Using PMVFAST, find the motion vectors:

bma -c current.jpg -p previous.jpg -a pmvfast -v motion.mv

Using the provided evaluation script, evaluate.py, we can generate the motion vectors and motion compensated frames from the video below. The actual video tested (preview below) was 1920×1080, 385 frames at 30 fps and the block size was set to 8×8. Use of temporal neighbours was not implemented in PMVFAST and both methods could have been accelerated by using SIMD and multithreaded programming techniques.

Ferry Test Sequence

Video Sequence Used for Testing


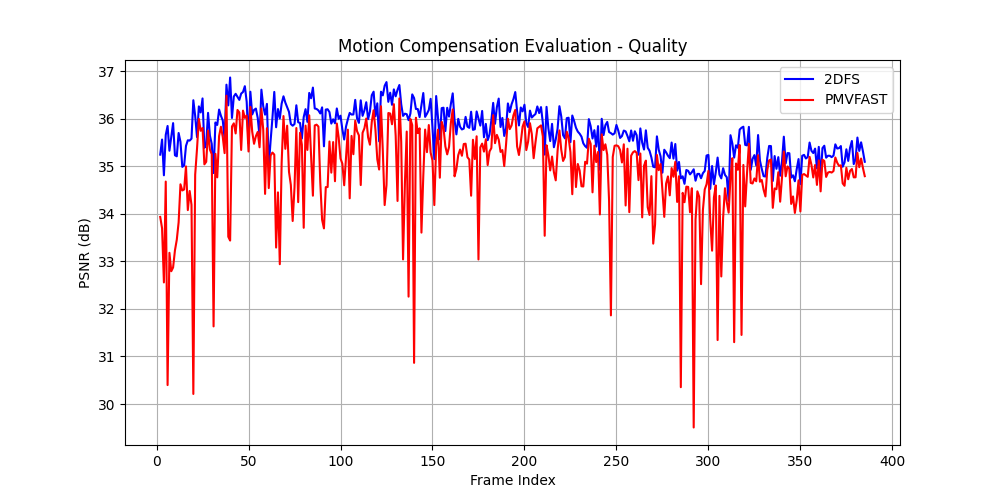
PSNR Comparison of Motion Estimation Algorithms
MethodAverage PSNR (dB)Average Time (secs)
2DFS35.7230.5
PMVFAST34.910.28

Peak Signal to Noise Ratio (PSNR) is a metric for comparing images. Above 30 dB it becomes more difficult to spot artefacts. Above 40 dB you usually need to zoom to find artefacts and compression noise (during capture) and sensor noise are at a similar scale to motion estimation artefacts.

Most of the artefacts visible in the motion compensated video are at the edges of the frame, i.e. not possible to compensate from motion alone.

Despite PMVFAST dropping in quality at various times; almost all frames were recovered at greater than 30 dB. In a video codec, residual coding will make up for poor motion vectors and edge effects; furthermore, a rate-distortion mechanism will trade off quality to achieve the desired bit rate for the final video stream.

Summary

Optical Flow Estimation

Introduction

Optical flow describes the apparent 2D motion of pixels in a video frame. There are several methods for estimating per-pixel motion, the simplest method would be to match a neighbourhood of pixels surrounding a central pixel with a similar neighbourhood in another frame. Optical flow methods use additional constraints, with the main being that the change in intensity of a moving pixel corresponds to the amount of motion in (x,y) and the amount of time that has passed.

Pros

Cons

Implementation

  Code on github

OpenCV implements Farnebäck's polynomial expansion based method for optical flow estimation. It matches polynomials fitted to local neighbourhoods of pixels. A global motion model is fitted under the assumption that local flow vectors vary slowly to aid robustness and the algorithm is run at multiscale to support large displacements.

RAFT (Recurrent All-Pairs Field Transforms) is a deep model for optical flow estimation. As the name suggests, the method matches all pixels in one image to all possible matches in the second image. Despite the computational cost, speed is kept high by working on downsampled features, re-using the all-pairs correlation, efficient refinement of flow vectors and GPU implementation.

Example

For testing, frames 150 and 149 of the Basketball sequence [*] will be used:

Frame 150
Frame 149

Using OpenCV's impementation of Farnebäck's method, find the optical flow between the two images:

ocv-of-single.py --current frame_00150.png --previous frame_00149.png --output flow-visualisation.png

The optical flow result:

Optical Flow from OpenCV

Optical Flow estimated using Farnebäck's method


In this visualisation of the optical flow vectors, the colour corresponds to the direction and the brightness corresponds to the vector magnitude.

You can extract all images from a video to a directory, compute optical flow for all consecutive image pairs, and save images visualising the flow using this script:

ocv-of-sequence.py --video input.mp4 --frames extracted_frames -o flow

Images from the video will be saved into the extracted_frames directory and visualisation images into the flow directory:

PyTorch contains the RAFT model in the torchvision module. To use RAFT, we must,

This is implemented in Python based on the PyTorch tutorial for RAFT; two scripts process either a single pair of frames or a video sequence. The scripts are raft-of-single.py and raft-of-sequence.py; they take the same parameters as the OpenCV scripts above.

Here is the optical flow estimated for the same Basketball images,

Optical Flow from RAFT

Optical Flow estimated using RAFT


Although this result looks better, we need to compare in an objective way. To make a comparison between Farnebäck's method and RAFT, frame 149 from the basketball sequence was compensated using the optical flow and PSNR was calculated against frame 150.

As RAFT estimates flow at a lower resolution (960×520) to the source video (1280×720), the PSNR was computed after resizing the image.

The compensated image was resized using ImageMagick convert, i.e. 

convert -resize 1280x720! compensated.png compensated_1280x720.png

MethodPSNR (dB)
Farnebäck22.5025
RAFT31.8379

The flow from the whole sequence was also computed, as previewed below.

RAFT optical flow for the Basketball sequence

Optical Flow for the Basketball Sequence


Summary

References

Credit

Basketball sequence from pexels.com, by Pavel Danilyuk, downloaded via PyTorch.